(1. 苏交科集团股份有限公司, 江苏 南京 211112; 2. 南京工业大学, 江苏 南京 211816;3.
南京市公路事业发展中心, 江苏 南京 210008)
引 言
近年来随着桥梁工程工业化和标准化的发展,装配式桥墩因其工厂化预制、环境影响小、施工速度快、安全性高等优点在国内外得到了越来越广泛的应用[1]。装配式桥墩需要解决的关键技术问题是预制构件之间的连接方式。目前常见的连接方式有现浇湿接缝连接、预应力连接、承插式连接、灌浆波纹管连接、灌浆套筒连接等[2-3]。其中灌浆套筒连接最早由美籍华裔科学家余占疏博士于20世纪60年代发明[4],经过几十年的推广,目前灌浆套筒连接在装配式建筑中得到了较为广泛的应用,在装配式桥墩中的推广应用相对较晚。1992年,美国弗洛里达州的Edison桥首次采用了这种连接形式[5];2012年,我国在上海S6公路工程中首次运用该种预制桥墩[6],此后,灌浆套筒连接的预制桥墩陆续在上海、江苏、湖南等地推广应用[7]。
针对灌浆套筒连接的装配式桥墩,国内外很多学者已经开展了一部分试验和理论研究[8-12]。文献[8]通过与传统现浇桥墩的对比,发现该种连接形式可以取得类似于现浇桥墩的抗震性能,达到“等同现浇”的设计效果。文献[9]发现钢质套筒的位置对抗震性能影响较大,将套筒布置在墩身底部会导致刚度变大,使塑性铰区转移至套筒顶面;将套筒布置在承台内比布置在墩身内有助于获得良好的抗震效果。文献[10]进行了5组拟静力试验,发现采用灌浆套筒连接的预制拼装桥墩主要表现为弯剪破坏模式,截面中心增设无黏结预应力筋的试件,可提高抗剪承载力,并降低残余变形。文献[11]对比了灌浆套筒连接形式与灌浆波纹管连接形式,研究结果表明,套筒连接装配式桥墩的位移延性与累积耗能能力优于金属波纹管连接的装配式桥墩。文献[12]建立了节段式桥墩受力性能的数值分析方法,并对轴压力、砂浆强度等因素进行了参数分析。
从上述的研究可以发现,研究连接部位构造参数对套筒连接桥墩的抗震性能的影响具有十分重要的工程意义,但是大部分学者受试件数量限制,涉及的参数较少。本文以套筒连接的预制装配式桥墩为对象建立了实体有限元模型,通过数值模拟的方法,对可能影响抗震性能的套筒长度、套筒厚度和配箍率等构造参数进行了分析,对已有研究进行了补充,以期对实际工程的设计提供参考。
1 计算参数
以某工程采用的装配式单柱墩为依托,按1∶5的比例对桥墩进行缩尺研究,每个模型由三部分组成,由上到下分别为加载端、墩身和基础。整个模型高2900
mm,墩身高1800 mm,加载点至接缝面距离为2000 mm;墩柱截面为正方形,尺寸为400 mm×400
mm;纵向钢筋为12根直径18 mm的HRB400钢筋;箍筋为HRB400,直径8 mm。
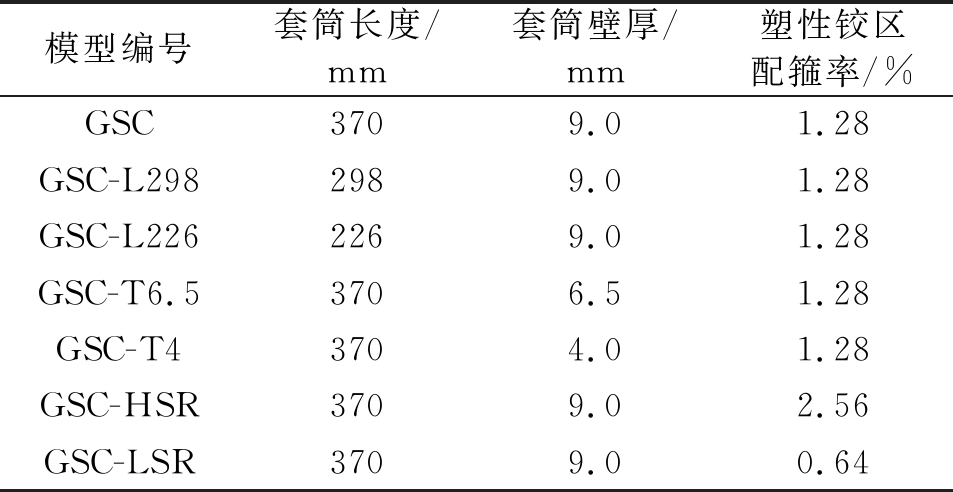
主要研究套筒长度、套筒壁厚和塑性铰区配箍率对桥墩抗震性能的影响,利用有限元软件ABAQUS建立7个有限元模型对其抗震性能进行了数值分析,具体参数如表1所示。其中GSC为原型模型,表示套筒布置在预制墩身底部(Grouting-sleeve-column)的预制桥墩。文献[13]规定钢筋插入套筒的锚固长度不应小于8d(d为钢筋直径),文献[14]规定钢筋插入套筒的锚固长度不应小于10d,本次研究取钢筋插入深度为10
d,8 d和6 d,对应套筒长度参数为370,298和226
mm,分别对应GSC、GSC-L298和GSC-L226模型。文献[15]规定套筒壁厚不应小于4
mm,本次研究取套筒壁厚为9,6.5和4
mm,分别对应GSC、GSC-T6.5和GSC-T4模型。此外,GSC-HSR模型塑性铰区体积配箍率为2.56%,GSC-LSR模型塑性铰区体积配箍率为0.64%,其余参数与原型模型保持不变。
表1 模型参数
本次预制装配式单柱墩的抗震性能分析运用实体有限单元法,通过有限元软件ABAQUS进行模拟[16]。混凝土采用缩减积分八节点实体单元(C3D8R),灌浆套筒等效为梁单元(B31),钢筋采用桁架单元(T3D2);混凝土本构模型采用塑性损伤模型(CDP模型),灌浆套筒本构模型采用理想弹塑性模型,钢筋本构模型采用双折线模型;将钢筋内置在混凝土中,套筒与钢筋和混凝土之间均采用Tie连接方式;将基础在底部进行固结处理并假定其为刚性结构。数值模拟采用位移控制加载方式,位移比δ定义为加载点水平位移与加载点到接缝面垂直距离的比值,按位移比0.2%的倍数进行单周往复加载,当δ达到6%时终止模拟。
2 计算结果2.1 套筒尺寸的影响
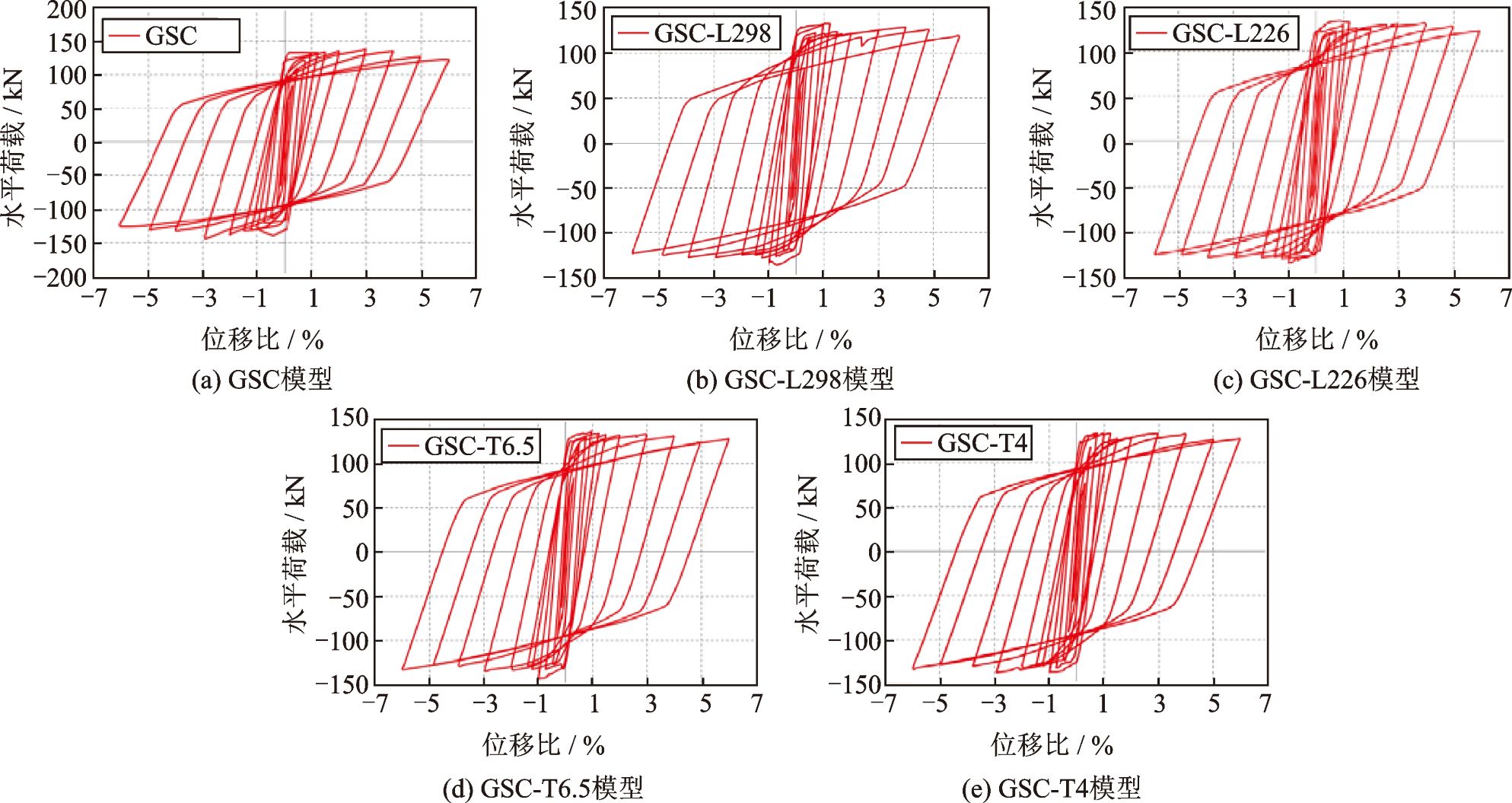
为了研究套筒的连接性能,目前很多学者通过改变套筒尺寸来提高灌浆料与钢筋粘结强度[17-18],但是针对预制桥墩整体抗震性能尚缺乏系统研究。根据ABAQUS的分析数据,分析了不同套筒尺寸下预制桥墩的滞回曲线及骨架曲线,然后进一步分析了塑性铰区域的变化,比较了不同套筒尺寸下的预制桥墩抗震性能的差异。
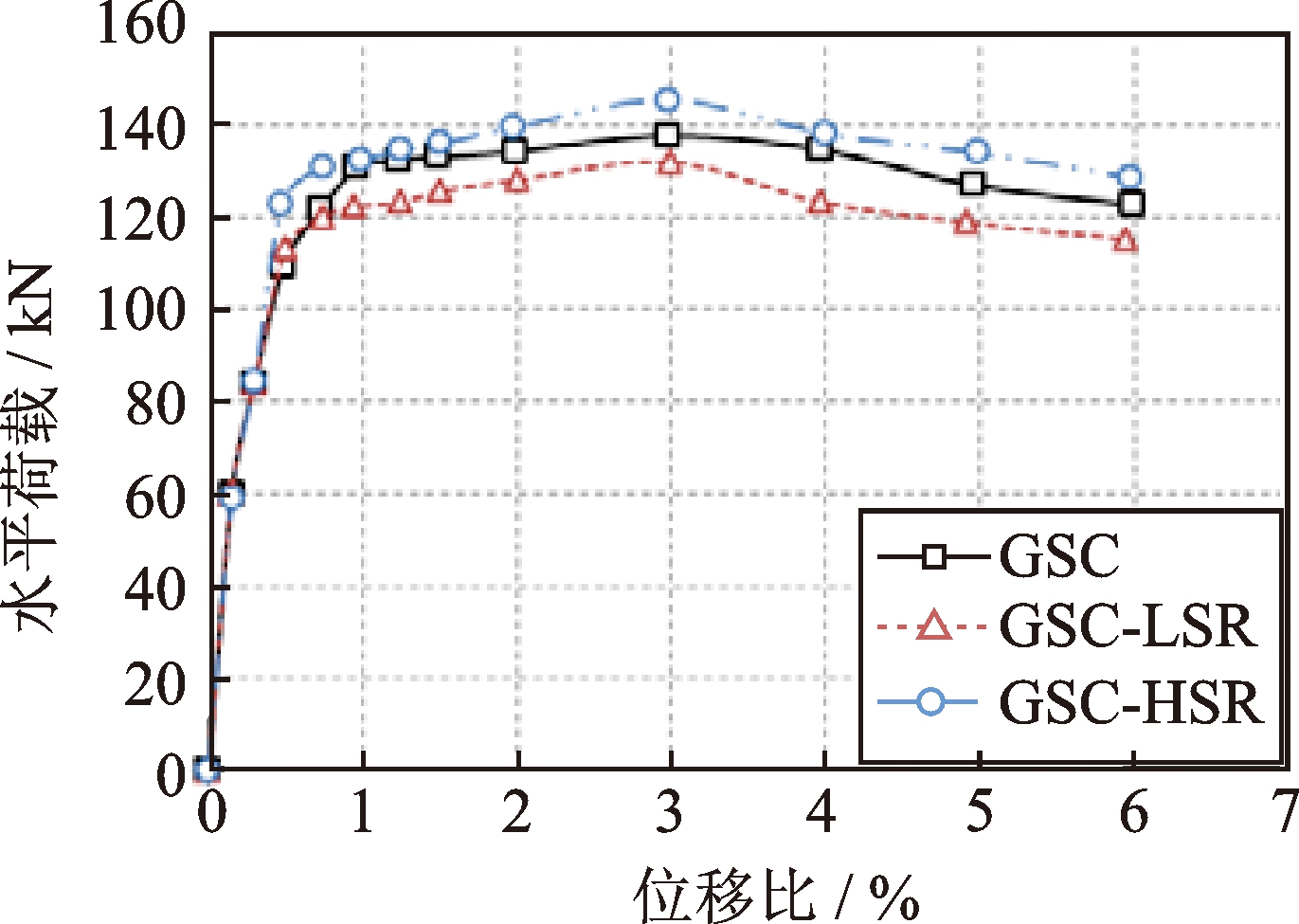
计算所得预制桥墩的滞回曲线如图1所示。可以看出,不同模型的滞回曲线均比较饱满,说明5种模型构件都具有较强的变形能力。改变套筒尺寸后滞回曲线变形趋势一致,改变套筒尺寸并不会显著影响耗能能力和自复位能力。将模型在每个滞回环最大的荷载值取点,连成如图2所示的骨架曲线,并通过计算得到相应指标如表2所示,反映了模型的承载力特征。可以看出,增大套筒长度和厚度,模型最大承载力会随之上升。GSC模型的最大承载力比GSC-L298、GSC-L226模型分别高出4.2%和4.4%,比GSC-T6.5、GSC-T4模型分别高出1.1%和3.5%,等效屈服荷载基本相近。模型初始刚度随套筒长度和壁厚增加而呈增大趋势,而屈服刚度和屈服后刚度无明显变化规律。总体来看,可以发现各模型的各指标差别不大。所以改变套筒尺寸,对结构的抗震性能影响不大。
表2 不同套筒尺寸模型骨架曲线指标

注:δy为屈服位移比,Fy为屈服荷载,δm为模型达到极限承载力时对应的位移比,Fm为极限承载力,K0为初始刚度,K1为屈服刚度,K2为屈服后刚度。
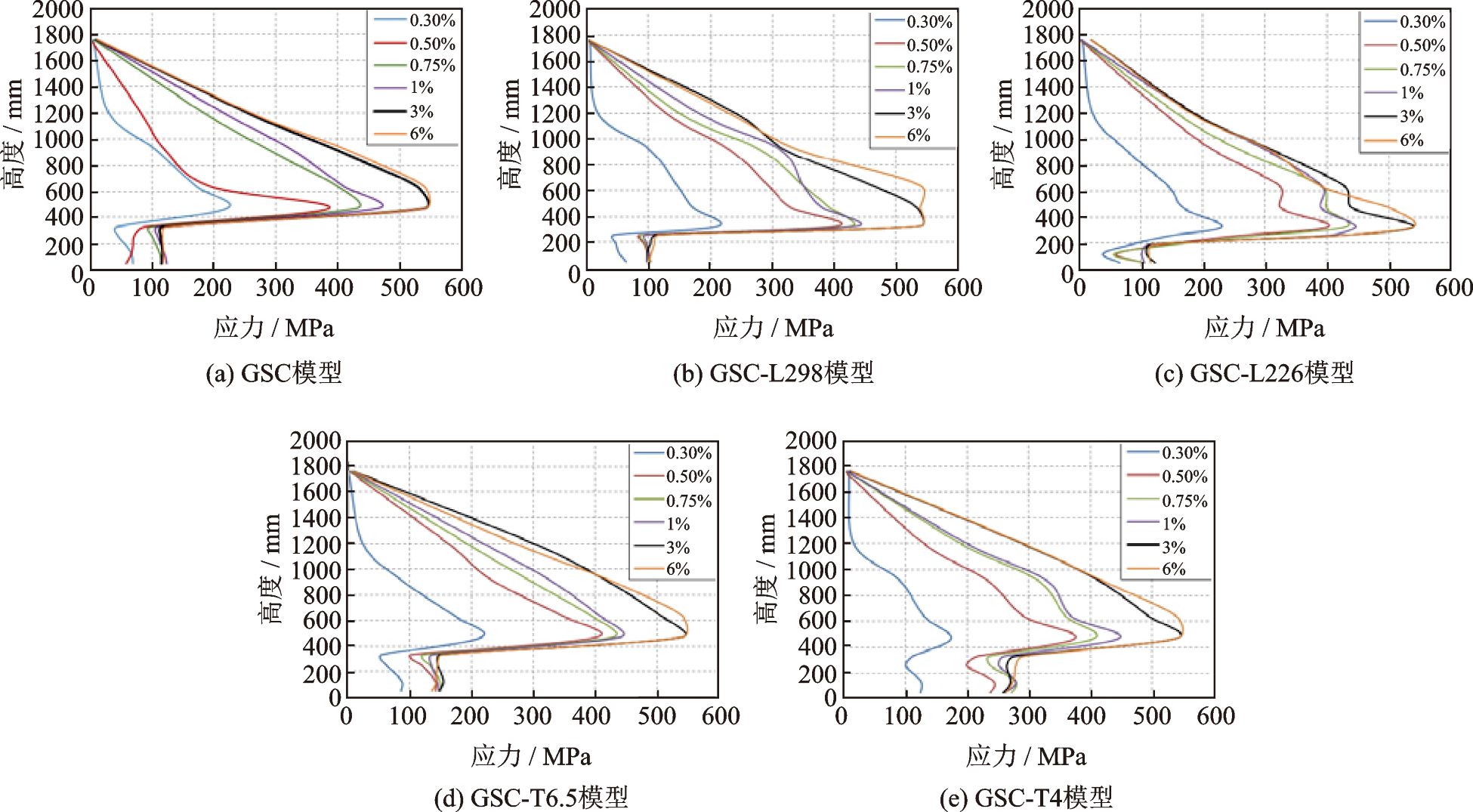
图3为各模型墩柱内主筋在不同加载位移比下的应力大小。由图3可知,主筋应力随着加载位移的增加而增加,随着位置高度的降低而增加,在套筒处应力又急剧减小。加载初期,应力随加载位移的增大而增大;加载中后期其应力基本保持不变。GSC模型的套筒内应力最大达到124
MPa,GSC-L298模型的套筒内应力最大达到116 MPa,GSC-L226模型的套筒内应力最大达到153
MPa,套筒高度对应力影响并不明显。随着套筒壁厚的减小,其套筒上应力随之增加,GSC-T6.5模型的套筒内应力最大达到155
MPa,GSC-T4模型的套筒内应力最大达到290 MPa,较GSC模型增大133.9%,但所有套筒内应力均远小于套筒550
MPa的抗拉强度,说明钢筋与套筒锚固效果良好,套筒规格均能满足应力要求。
对于钢筋混凝土墩柱,由于材料复杂且各向异性,当墩柱在侧向力作用下发生塑性变形,弯矩最大处集中在一段区域中,该段区域即为墩柱的塑性铰区。试验中一般可以通过观察墩底混凝土剥落范围来大致确定塑性铰区域,在数值模型中通过钢筋屈服范围确定塑性铰区域,即纵筋屈服法。纵筋屈服法是指墩柱在往复荷载推拉过程中,沿墩柱高度方向的纵筋会陆续屈服,形成了一个纵筋的屈服区域,将这个区域定义为塑性铰区域。在模拟中提取不同位移比下的沿墩高方向的纵筋应力值,当墩柱破坏后(即加载后期),选取应力最大的纵筋,并沿着墩高读取应力值,将应力大于屈服应力的区域作为塑性铰区域。根据图3中应力变化,塑性铰长度计算如表3所示。由表3比较可知,预埋在墩身内的套筒如果长度增大会使塑性铰区呈上升趋势;而相同套筒长度下壁厚增大会减小塑性铰高度。
表3 塑性铰长度
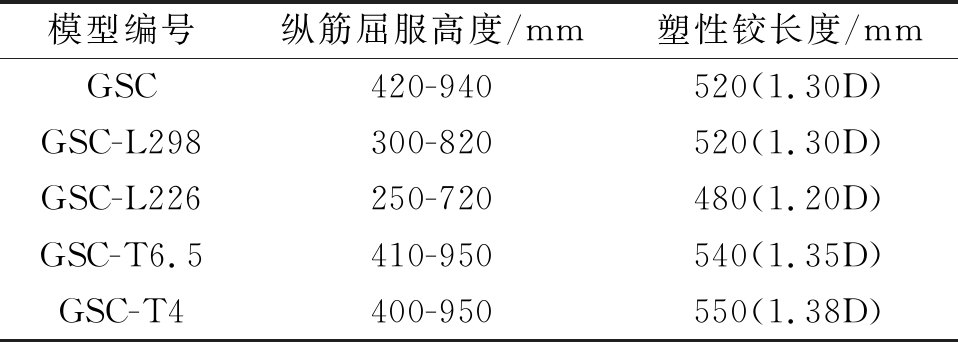
注:D为墩柱宽度。
2.2 配箍率的影响
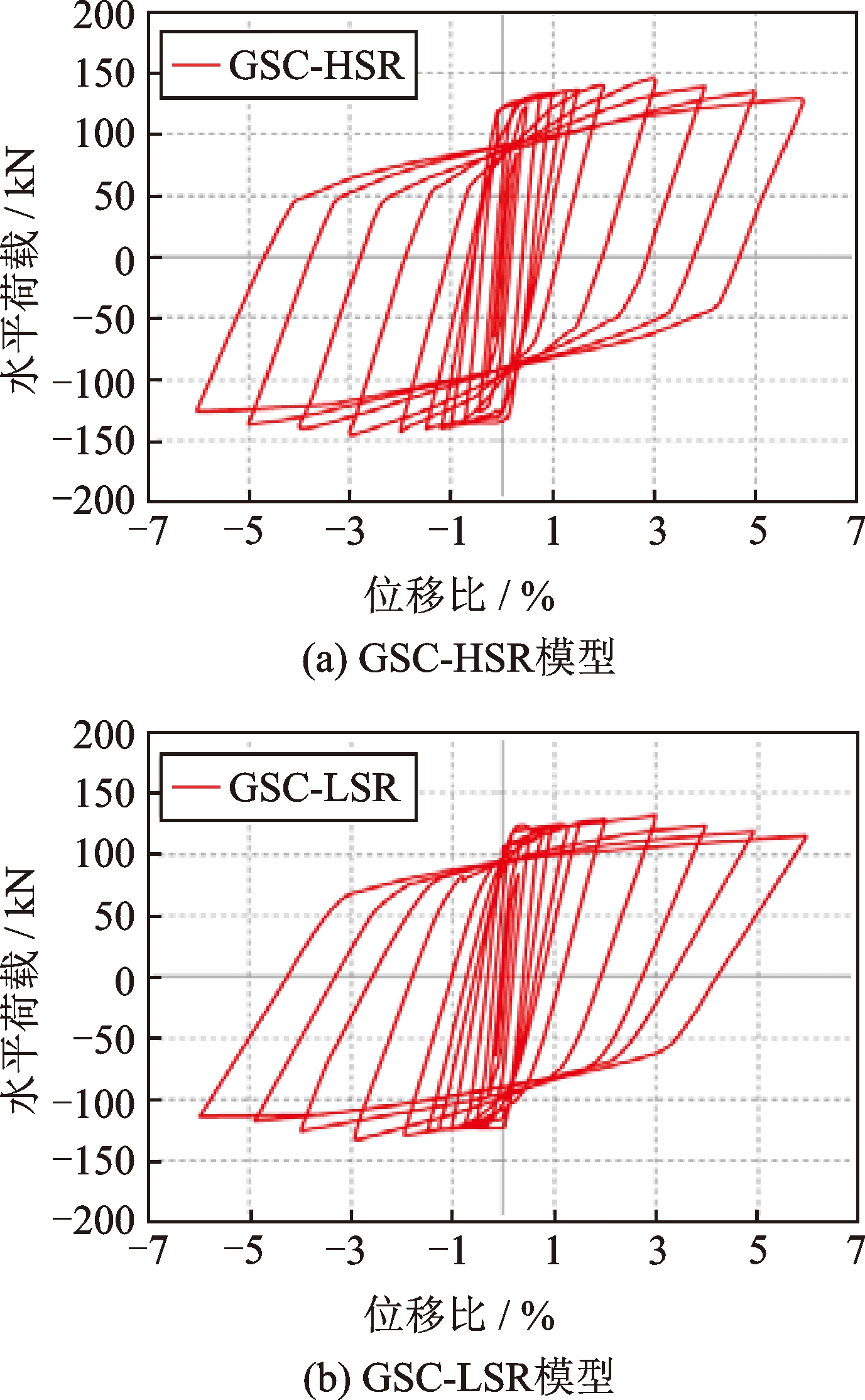
文献[19]的试验结果表明:套筒预埋在墩身中的试件在套筒位置刚度大,套筒高度范围内裂缝很少,裂缝集中于接缝和套筒顶部2个区域。因此判断,增加塑性铰区的配箍率可以提高墩柱承载能力。为验证这一点,将配箍率也作为影响参数进行分析。根据ABAQUS的分析数据,不同塑性铰区配箍率下预制桥墩的滞回曲线及骨架曲线如图4和图5所示,各试件的骨架曲线指标如表4所示。
表4 不同配箍率模型骨架曲线指标

注:δy为屈服位移比,Fy为屈服荷载,δm为模型达到极限承载力时对应的位移比,Fm为极限承载力,K0为初始刚度,K1为屈服刚度,K2为屈服后刚度。
从图4滞回曲线可以看出,配箍率发生变化,对滞回曲线影响不大,各模型滞回曲线趋势基本一致。从图5骨架曲线可以看出,各模型在峰值荷载前骨架曲线基本重合,峰值荷载后由于箍筋对混凝土的约束强度不同,骨架曲线开始出现变化,骨架曲线高度随着配箍率的增大而增大。随着配箍率每增大一倍,峰值荷载将增加4.3%及5.5%,屈服荷载将增加3.5%及6%。另一方面,刚度指标变化幅度较小,这是由于套筒的存在增大了底部刚度,对区域内混凝土保护较好,这与试验结果相吻合。
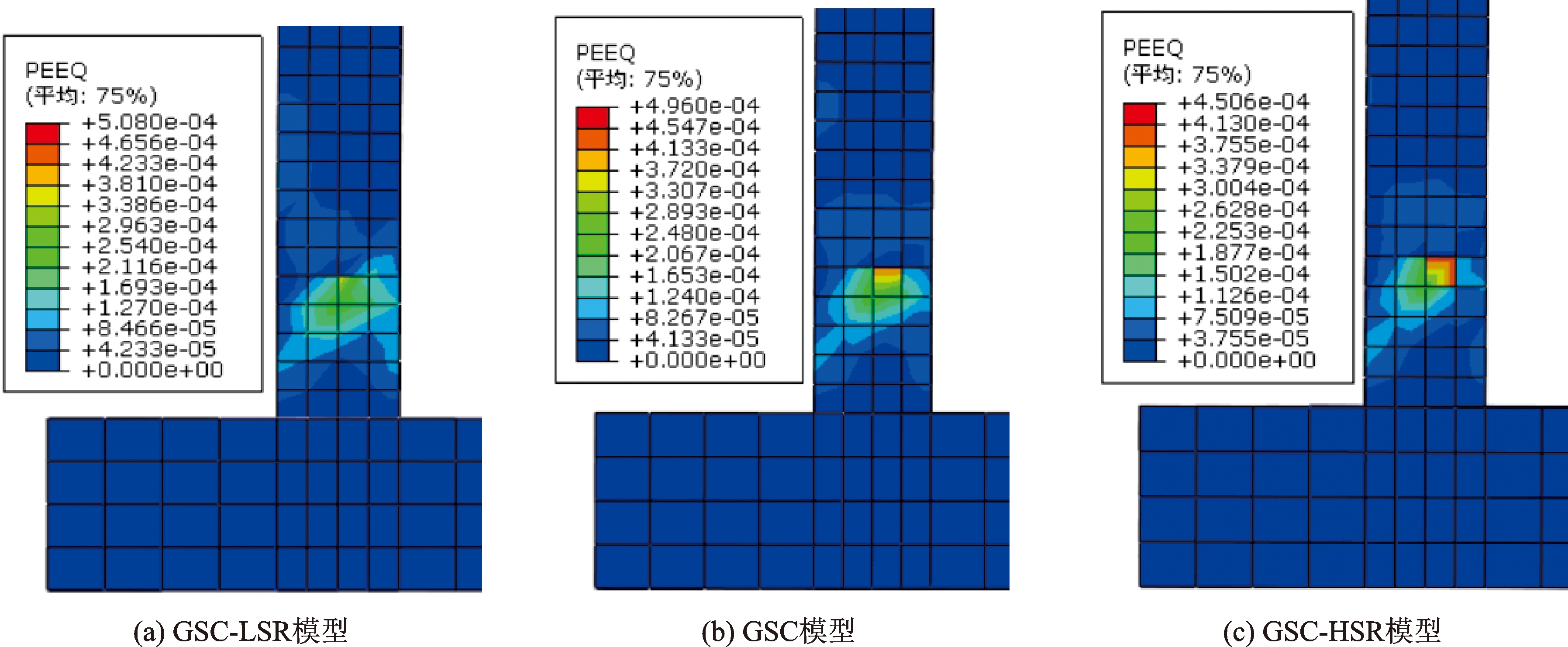
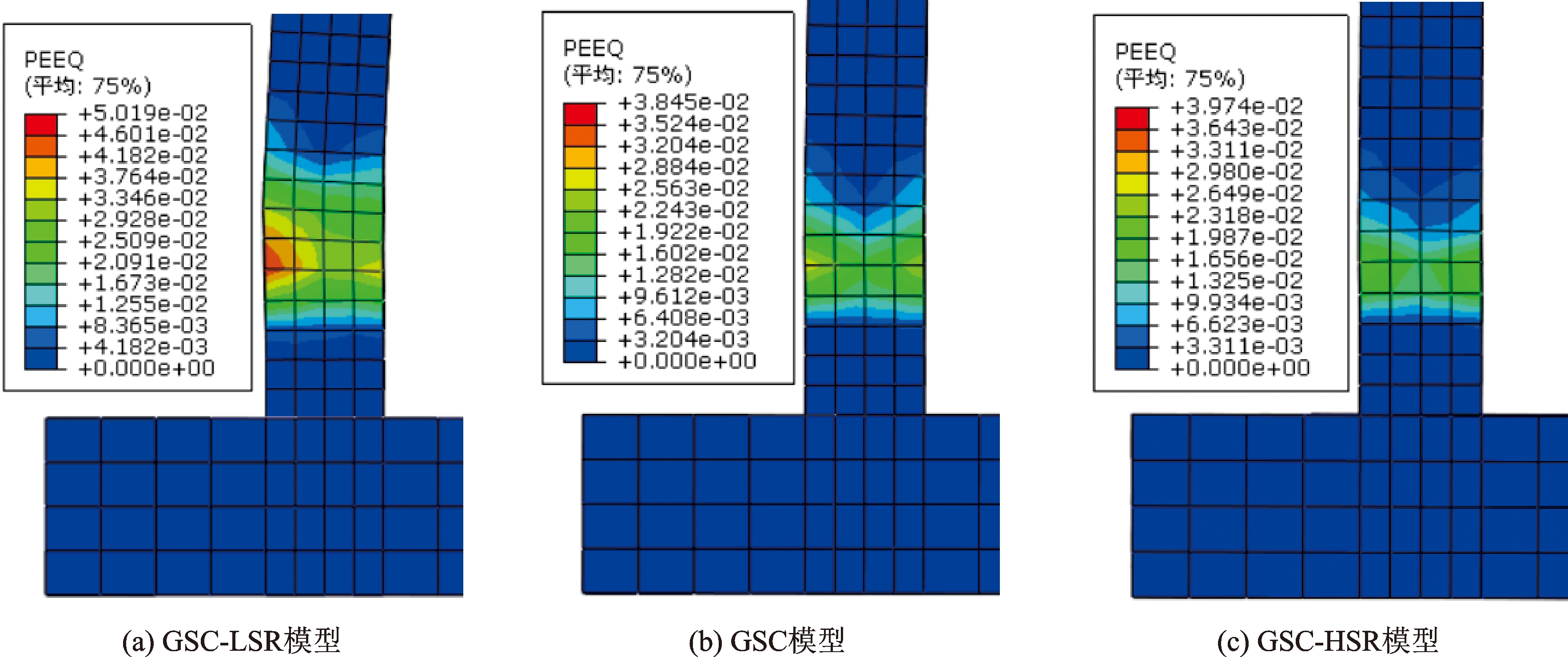
由于配箍率不同对塑性铰区混凝土具有不同的约束效应,继续研究各模型混凝土塑性应变的分布情况,如图6-7所示。由图6可以看出,各模型等效塑性应变分布在套筒以上墩柱中间部位,有向四周发展的趋势。当GSC-LSR模型破坏时,如图7(a)所示,等效塑性应变区域分布高度明显增大,且分布不均匀,墩柱左侧分布范围较大,说明GSC-LSR模型因配箍率较低,容易发生弯剪破坏。当GSC模型和GSC-HSR模型达到破坏后,其等效塑性应变分布如图7(b)和图7(c)所示,其等效塑性应变分布不同于GSC-LSR模型,两模型墩柱左右两侧分布均匀,呈Y型。综合对比各模型混凝土的等效塑性应变分布,可以发现,GSC模型和GSC-HSR模型等效塑性应变分布高度明显小于GSC-LSR模型,而GSC-HSR模型等效塑性应变分布高度小于GSC模型,说明配箍率增加后,箍筋对混凝土的约束作用也在提高,墩柱在往复荷载作用下混凝土开裂后,箍筋可以更有效地承担剪力,保证墩柱有较高的抗剪承载力以抵抗地震作用,建议配箍率保持在1.28%-2.56%。
3 结 论
(1)套筒高度变化不能显著影响套筒上应力大小,但随着套筒壁厚的减小,其套筒上应力随之增加。墩柱塑性铰区会随着套筒长度的增加而上移,塑性铰长度在1.2D-1.38D之间变化。
(2)塑性铰区配箍率增加后,墩柱混凝土等效塑性应变分布高度相对减小,箍筋对塑性铰区混凝土的约束作用在提高,墩柱在往复荷载作用下混凝土开裂后,箍筋可以更有效地承担剪力,保证墩柱有较高的抗剪承载力以抵抗地震作用。
(3)总体来说,在规范允许范围内改变套筒尺寸,对结构的抗震性能影响不大。增大配箍率,可以提高一定的承载力,但对结构刚度影响较小,配箍率宜保持在1.28%-2.56%。
参考文献:
[1] Culmo M P. Accelerated bridge construction-experience in
design, fabrication and erection of prefabricated bridge elements
and systems[R]. FHWA-HIF-12-013, 2011.
[2] Culmo M P. Connection details for prefabricated bridge elements
and systems[R]. FHWA-IF-09-010, 2009.
[3] 项贻强, 竺 盛, 赵 阳.快速施工桥梁的研究进展[J].中国公路学报,2018,31(12):1-27.
[4] YEE A A,ENG H D. Structural and economic benefits of
precast/prestressed concrete construction[J].PCI Journal, 2001,
46(4):34-42.
[5] FHWA. Connection details for prefabricated bridge elements and
systems: FHWA-IF-09-010 [S]. McLean, V. A.: Federal Highway
Administration, 2009.
[6] 黄国斌,查义强.上海公路桥梁桥墩预制拼装建造技术[J].上海公路,2014,(4): 1-5.
[7] 赵松华,李国平.节段预制拼装桥墩技术及其应用[C].第二十二届全国桥梁学术会议论文集.2016:374-384.
[8] 樊
泽,曾明辉,胡志坚.预制拼装桥墩连接构造抗震性能分析[J].武汉理工大学学报(交通科学与工程版),2019,43(2):357-362.
[9] Haber Z B,Mackie K R,AI-Jelawy H M.Testing and analysis of
precast columns with grouted sleeve connections and shifted plastic
hinging[J].Journal of Bridge Engineering,2017,22(10):04017078.
[10]
王志强,张杨宾,蒋仕持,等.套筒连接的预制拼装桥墩抗剪性能试验[J].同济大学学报(自然科学版),2018,46(6):767-775.
[11] 黄 宜,邱文亮,黄才良,等.单节段装配式桥墩抗震性能试验研究[J].大连理工大学学报,2016,56(5):481-487.
[12] 胡 皓.节段预制拼装桥墩接缝承载能力的影响因素分析[J].工业建筑,2020,50(3):88-95.
[13] 钢筋套筒灌浆连接应用技术规程(附条文说明):JGJ 355-2015[S].2015.
[14] 预制拼装桥墩技术规程:DG/TJ 08-2160-2015[S].2015.
[15] 钢筋连接用灌浆套筒:JGT 398-2012[S].2012.
[16] 程中娜.基于ABAQUS的智能有限元分析前处理技术研究[D].济南:山东大学, 2017.
[17] 张增德,赵春风,丁敬华,
等.预制装配式结构GFRP灌浆套筒设计与数值分析[J].合肥工业大学学报(自然科学版),2019,42(1):81-87.
[18] 余
琼,孙佳秋,袁炜航.带肋钢筋与套筒约束灌浆料黏结性能试验[J].哈尔滨工业大学学报,2018,50(12):98-106.
[19] 魏红一,肖 纬,王志强,
等.采用套筒连接的预制桥墩抗震性能试验研究[J].同济大学学报(自然科学版),2016,44(7):1010-1016.